
一、前言
在矩陣單元的教學中,學生常會問兩個問題:
(1) 矩陣乘法為何如此定義?
(2) “線性”變換中“線性”一詞的意義為何?
在中央大學單維彰教授、國家教育研究院鄭章華研究員的指導下,透過「十二年國民基本教育數學素養導向教材研發」計畫,針對學生問題,進行活動教材設計並進行試教。
本教材預設學生的先備知識:已學過矩陣加、減、係數積與乘法的運算。
試教對象:臺北市建國高中高二學生
本教材編寫過程雖盡心盡力,但難免仍有許多需要改進之處,還望教師、讀者給予指教。
由於篇幅限制在此僅提供部分教材與活動設計,至於其他各更多內容請參閱下列網址:https://www.naer.edu.tw/ezfiles/0/1000/img/67/165235000.pdf
二、教材活動設計理念與內容
教材設計理念(一)
在平面上的線性變換課堂一開始,先從歷史的角度切入,希望透過輕鬆的筆調與故事性的方式,介紹矩陣乘法規則的由來,並導入線性變換的概念。並期望學生瞭解「數學是一種人類活動的結果,而不是一開始便是如此型態的結構,並能對數學與我們的社會、文化以及與其它各種不同學科之間的關係,提供更多的認識」。除了希望學生的學習可以更緊密連接線性變換與矩陣的歷史與應用的脈絡之外,也期盼能提升學生數學閱讀的能力。
教材內容(一) 以數學史引起動機 :矩陣的乘法規則是怎麼定義出來的
|

|
1857年,英國數學家凱萊(Arthur Cayley,1821~1895)發表一篇被公認為近代矩陣理論和線性代數基石的論文〈矩陣理論備忘錄〉(A Memoir on the Theory of Matrices),他將矩陣從行列式抽離出來,視之為另一個數學物件,並且定義完備的矩陣代數運算。
而將矩陣以「Matrix」命名的是英國數學家西爾維斯特 (James Joseph Sylvester,1814~1897),「Matrix」有「母體、基礎」的意思,西爾維斯特可能意指 matrix 是行列式的「母體、基礎」,但他並未定義矩陣乘法。 |
凱萊曾經道出他研究方陣的動機,是為了簡化「線性變換」︰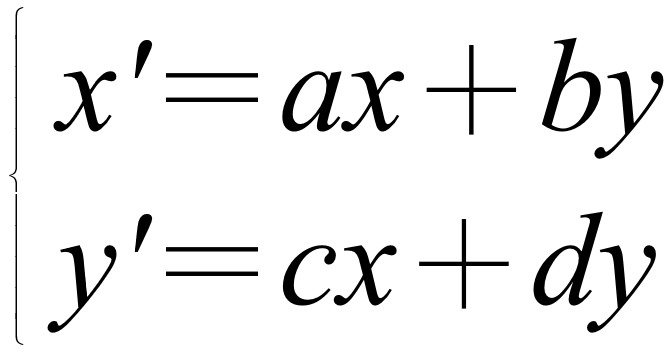 的描述和書寫。
的描述和書寫。
前面這個看起來很像二元一次聯立方程式的式子,其意義是把平面上的點(x,y)「變換」成另一個點( x',y' )。
令︰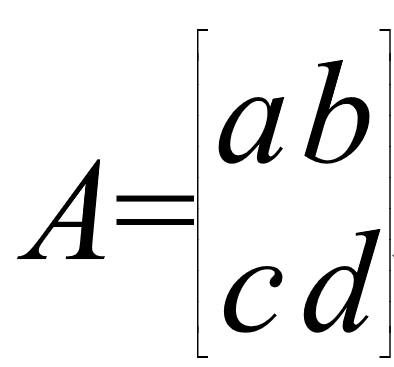 ,凱萊將上述的線性變換簡記成A, A後來被稱為是該線性變換的矩陣表示。
,凱萊將上述的線性變換簡記成A, A後來被稱為是該線性變換的矩陣表示。
1855年某日,凱萊考慮兩個「線性變換」①與②,其中
①: ,②:
,②:
考慮將平面上的點(x, y)先經過①的變換,再經過②的變換後成另一個點( x'',y'' )時,整理( x'',y'' )與(x, y)的關係,
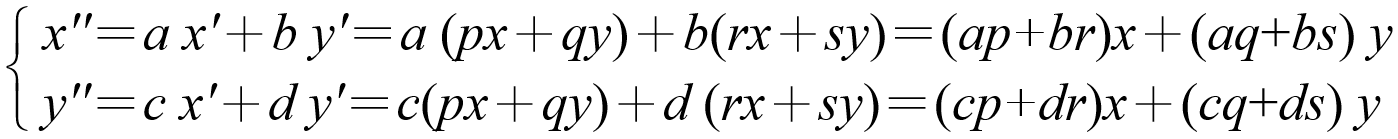 ,
,
得到 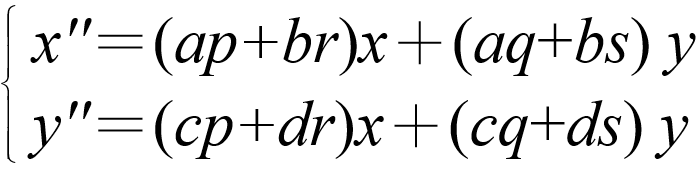
才氣洋溢的凱萊大膽構思,令 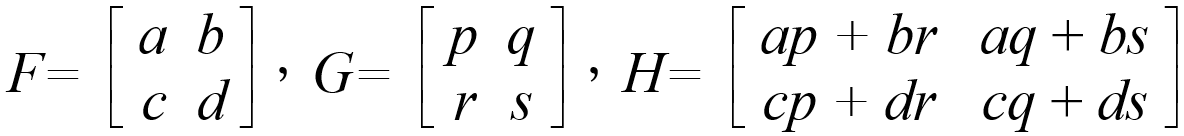 ,
,
將上述的變換過程以矩陣 和 「乘開」等於 表示,他興奮地寫下:
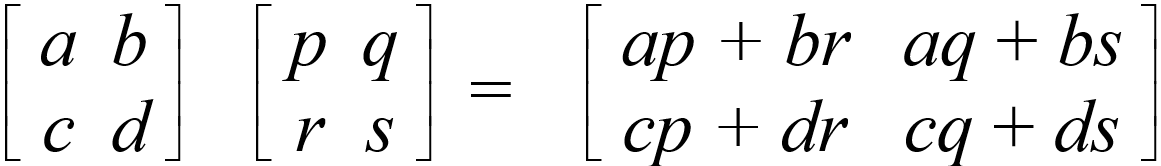
頓時矩陣乘法的運算規則誕生了!
參考資料
1. Arthur Cayley,1821~1895相片
[http://www-history.mcs.st-and.ac.uk/BigPictures/Cayley_5.jpeg]
2..單維彰,第490期科學月刊
3.線性代數的第一堂課──矩陣乘法的定義
[https://ccjou.wordpress.com/2010/06/18/%e7%b7%9a%e6%80%a7%e4%bb%a3%
e6%95%b8%e7%9a%84%e7%ac%ac%e4%b8%80%e5%a0%82%e8%aa%b2-
%e7%9f%a9%e9%99%a3%e4%b9%98%e6%b3%95%e7%9a%84%e5%ae%9a%e7%be%a9/]
4. 矩陣的故事 (The Story of Matrices),科學Online - 科技部高瞻自然科學教學資源平台,
[http://highscope.ch.ntu.edu.tw/wordpress/?p=32410]]
教材活動設計理念(二)
藉由【活動:海水運動是線性變換嗎?】,希望刺激學生思索線性變換更深層的意義,來對線性變換的幾何性質:保持共線與保持點之間距離的比例關係等,作學習與探討。
教材內容(二) 【活動:海水運動是線性變換嗎?】
引言 : 我們看海面上水的質點,考慮一分鐘以後這些質點的新位置。如圖中 原來是共線,但一分鐘後的新位置 若不再共線,這是平面上的一個運動,但它算不算是一種線性變換呢?
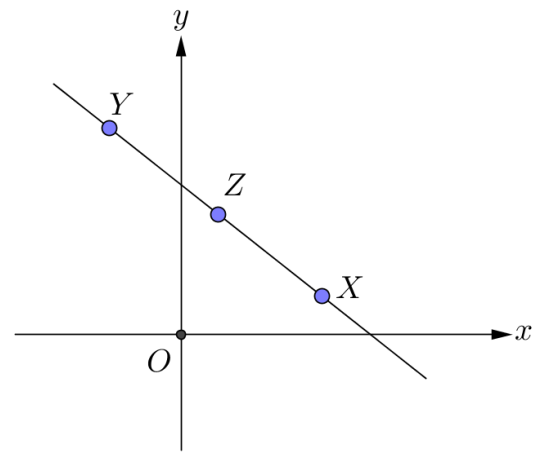 |
海水
運動
→
|
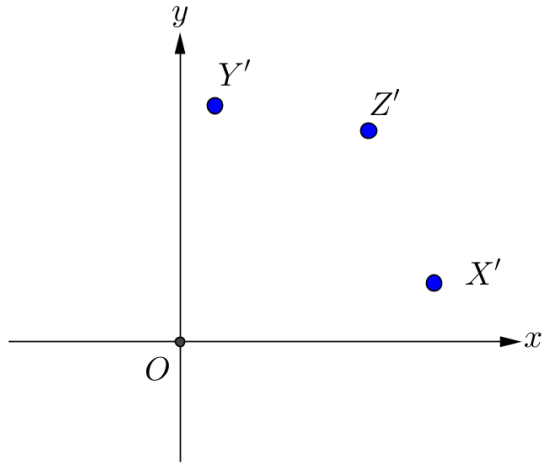 |
我們將透過本活動進行線性變換的幾何性質探討!
【活動:海水運動是線性變換嗎?】
【活動解答】略
綜合上述討論,可知二階方陣A在線性變換的意義下具有以下三個性質:
(LG1)將原點對應至原點。〔也就是說原點是平面上的一個固定點(fixed point)〕。
(LG 2)將共線三點P,Q,R,經過線性變換後所對應的三點P′,Q′,R′也共線。
且若 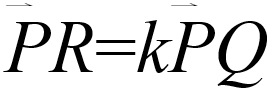 ,則
,則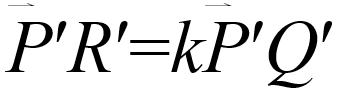 (即保持任兩點間距離的比例關係)。
(即保持任兩點間距離的比例關係)。
(LG 3)將直線變換成直線﹔將線段變換成線段。
這個結論可推廣至一般情形,就是
| 對於每一個“可逆的二階方陣”在線性變換的意義下具有(LG1)、(LG2)、(LG3)這三個性質。 |
因此前面所提的海水運動是沒有保持運動後的三點共線,所以不是一種線性變換!
由上述的性質,我們知道:
| 要決定一多邊形在線性變換下的圖形,我們只要將頂點的對應點求出,再以線段依次連結即可,而不用每一個點都得逐一求出它的對應點。 |
這將會方便我們在之後,去描繪各種線性變換下的多邊形圖形。
教材活動設計理念(三)
目前高中教材對線性變換的代數性質:
(1) 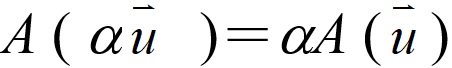 , (2)
, (2) 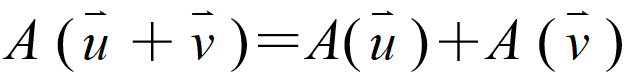 。
。
並不強調,這是連結大學線性代數的重要基礎,於是我們設計【活動:線性變換為什麼被稱作「線性」變換呢?】,透過之前學過的矩陣加法、係數積、乘法等運算規則,體會線性變換有「保持線性組合」效果,所以它被稱作「線性」變換。
教材內容(三) 【活動:線性變換為什麼被稱作「線性」變換呢?】
引言: 對平面上任一點P(x, y) ,由於矩陣 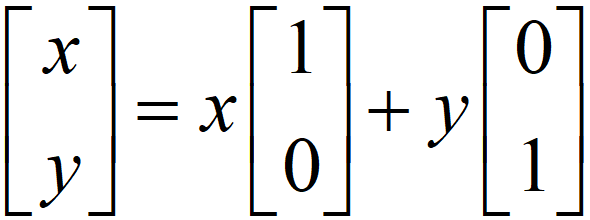
所以想要求點P(x, y)經 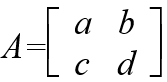 變換後的對應點P' ( x',y' )時,
變換後的對應點P' ( x',y' )時,
我們有另外一種觀點與方法:
由上面的式子,我們獲得兩件重要的訊息:
(1) 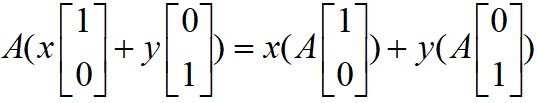 告訴我們:
告訴我們:
「點( 1,0 )與( 0,1 )線性組合的對應點」與「點( 1,0 )與( 0,1 ) 對應點的線性組合」相同。
也就是變換 A 有「保持線性組合」效果,所以它被稱作「線性」變換。
(2) 對應點P' ( x',y' )的另一種求法,可藉由「點( 1,0 )與( 0,1 ) 對應點的線性組合」求得!
我們將透過下面的活動來強化這些概念的學習。
【活動:線性變換為什麼被稱作「線性」變換呢?】
已知點( 1,0 )與( 0,1 )經二階方陣 作線性變換的對應點分別為( 2,-1 ),( 1,1 ),請問:
(1) 將點P( 4,3 )變換到哪裡?
(2)能否在不求出A的情形下,而得出點P的對應點? |
【活動解答】略
「保持線性組合」的好處
點P( 4,3 )的對應點P'的位置,可依下列方法找尋:
因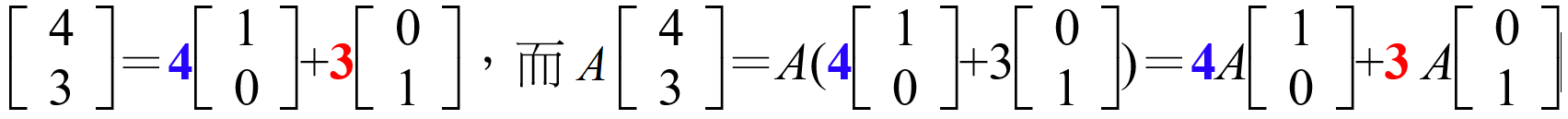
如圖所示,P'的位置可沿向量 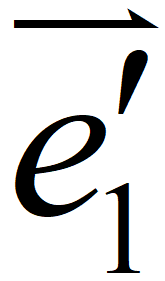 =( 2,-1 )走其4倍的距離,再沿向量
=( 2,-1 )走其4倍的距離,再沿向量 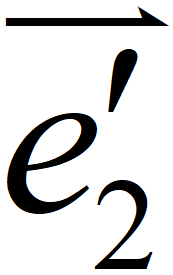 =( 1,1 )走其3倍的距離。此時停步,即為P經A變換後的新位置P'
=( 1,1 )走其3倍的距離。此時停步,即為P經A變換後的新位置P'
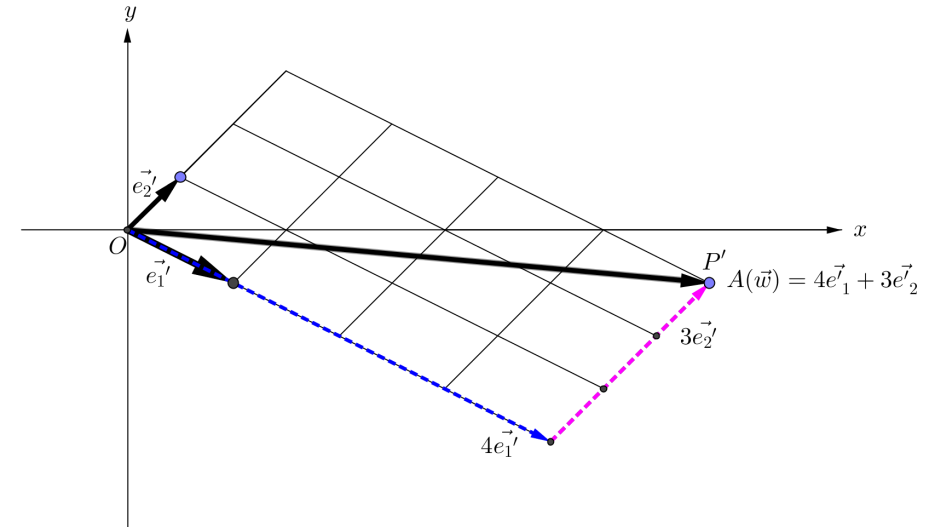
由上述討論可知:
|
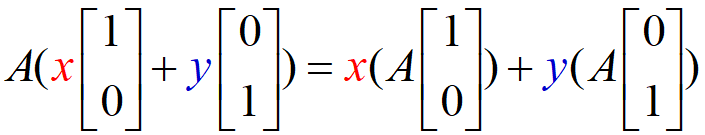 ,其中 x,y 為實數。 ,其中 x,y 為實數。
這表示
「點( 1,0 )與( 0,1 )線性組合的對應點」與「點( 1,0 )與( 0,1 )對應點的線性組合」相同。
所以線性變換A保持變換前後兩個點的線性組合之關係,故它被稱作「線性」變換。
|
一般而言,因為二階方陣A所表示的線性變換,可由點( 1,0 )與 ( 0,1 )的對應點所唯一確定且滿足下列兩個條件:
(1) A ( P+Q )=AP+AQ。
(2)A ( tP )=t( AP)。
其中P,Q分別是 ( 2×1 ) 階矩陣,其中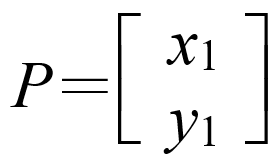 ,
,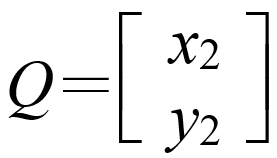 。
。
以上(1),(2)合稱為“線性條件”,是推廣線性變換定義的核心概念。這兩個條件對於「線性」的定義缺一不可。
--回目錄--
































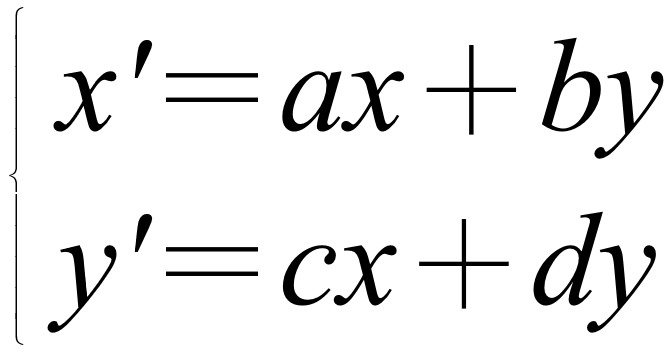 的描述和書寫。
的描述和書寫。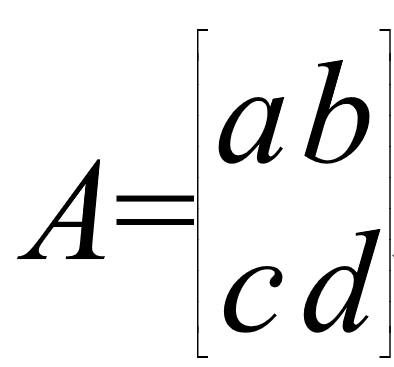 ,凱萊將上述的線性變換簡記成A, A後來被稱為是該線性變換的矩陣表示。
,凱萊將上述的線性變換簡記成A, A後來被稱為是該線性變換的矩陣表示。 ,②:
,②:
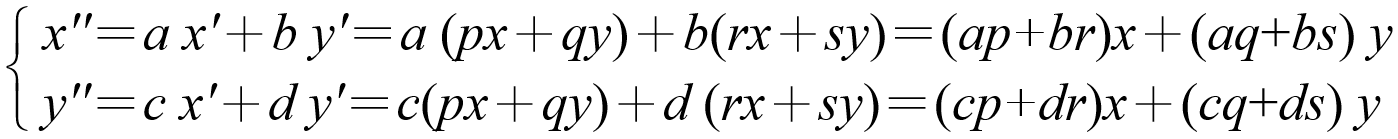 ,
,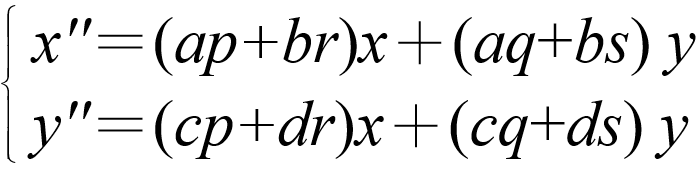
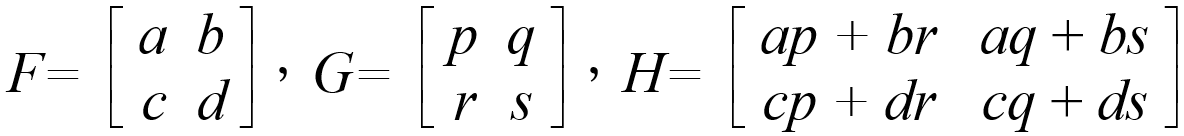 ,
,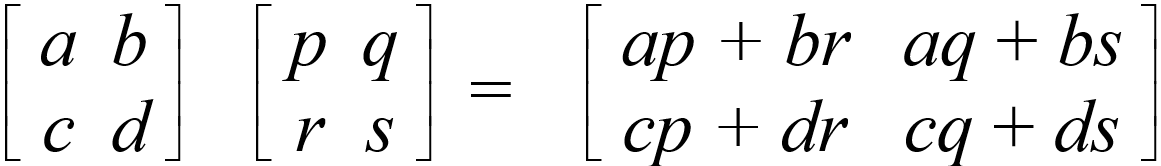


 所定義的線性變換分別將 O(0,0),P(1,0),R(-1,2)
所定義的線性變換分別將 O(0,0),P(1,0),R(-1,2)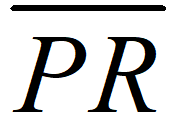 上找一點Q,使得
上找一點Q,使得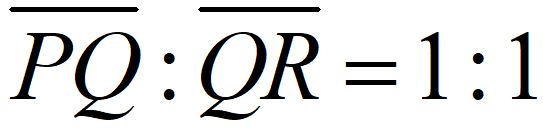 ,則
,則 ,請問
,請問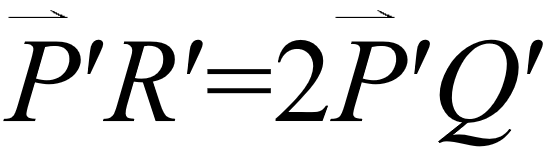 是否仍然成立?
是否仍然成立?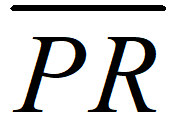 ”經由A變換後會是“線段
”經由A變換後會是“線段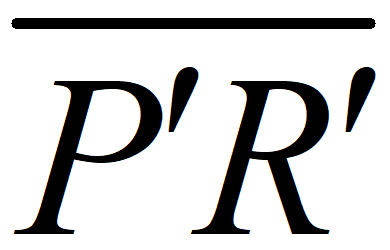 " 嗎?
" 嗎?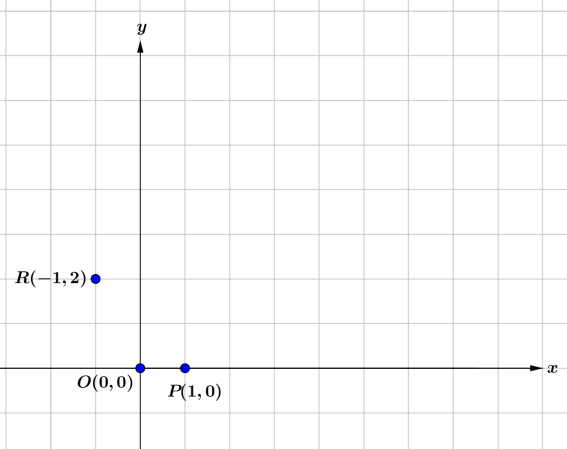
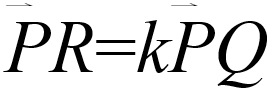 ,則
,則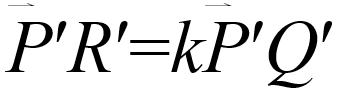 (即保持任兩點間距離的比例關係)。
(即保持任兩點間距離的比例關係)。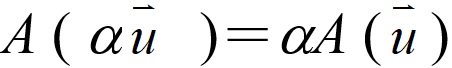 , (2)
, (2) 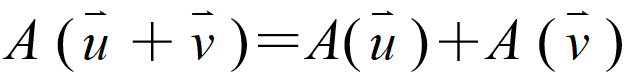 。
。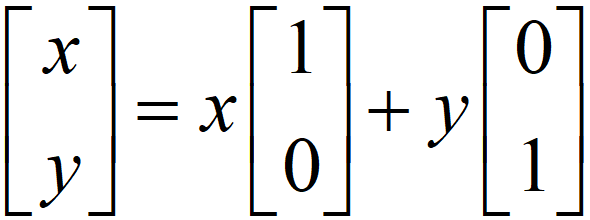
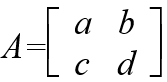 變換後的對應點P' ( x',y' )時,
變換後的對應點P' ( x',y' )時,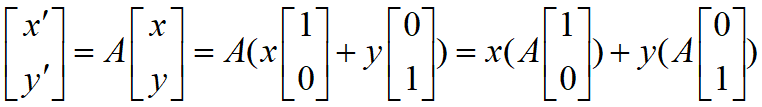

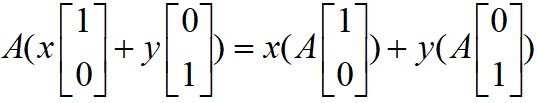 告訴我們:
告訴我們: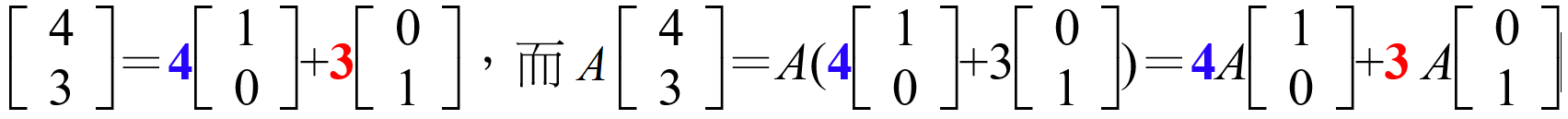
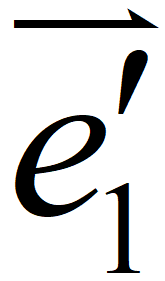 =( 2,-1 )走其
=( 2,-1 )走其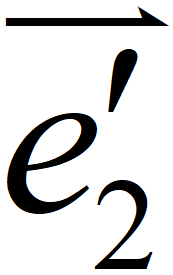 =( 1,1 )走其
=( 1,1 )走其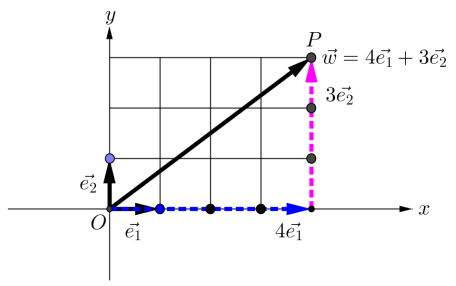
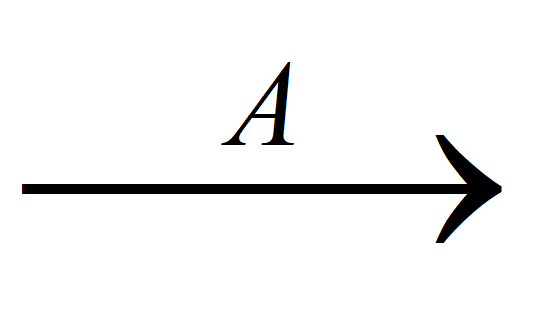
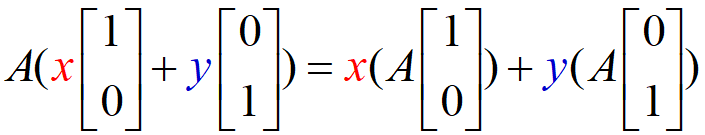 ,其中 x,y 為實數。
,其中 x,y 為實數。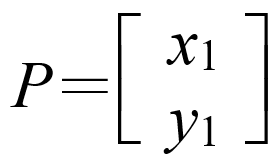 ,
,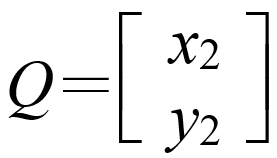 。
。














